Busca tu tema aquí - Google - Lizerindex®
25 octubre 2013
HOY TERREMOTO EN JAPÓN 25/10/13
Hoy 25/10/13, tsunami en Japón entre 6.8 y 7.5 grados
14 octubre 2013
LAS PROPOSICIONES
DEFINICIÓN DE LAS PROPOSICIONES
CLASIFICACIÓN DE LAS PROPOSICIONES
Las proposiciones se pueden clasificar en dos tipos:
Da clic para seguir el vínculo:
PROPOSICIONES SIMPLES O ATÓMICAS
PROPOSICIONES COMPUESTAS O MOLECULARES
PROPOSICIONES COMPUESTAS
Son también llamadas coligativas o moleculares; y se les llama así porque están compuestas por más de una proposición unidas por conectivos lógicos.Ver más...
Da clic para seguir el vínculo:
PROPOSICIONES CONJUNTIVAS
PROPOSICIONES DISYUNTIVAS
PROPOSICIONES CONDICIONALES
PROPOSICIONES BICONDICIONALES
PROPOSICIONES NEGATIVAS
Conectivos lógicos
PROPOSICIONES MOLECULARES
Son también llamadas compuestas o coligativas; y se les llama así porque están compuestas por más de una proposición unidas por conectivos lógicos.Ver más...
Da clic para seguir el vínculo:
PROPOSICIONES CONJUNTIVAS
PROPOSICIONES DISYUNTIVAS
PROPOSICIONES CONDICIONALES
PROPOSICIONES BICONDICIONALES
PROPOSICIONES NEGATIVAS
Conectivos lógicos
PROPOSICIONES COLIGATIVAS
Son también llamadas compuestas o moleculares; y se les llama así porque están compuestas por más de una proposición unidas por conectivos lógicos.Ver más...
Da clic para seguir el vínculo:
PROPOSICIONES CONJUNTIVAS
PROPOSICIONES DISYUNTIVAS
PROPOSICIONES CONDICIONALES
PROPOSICIONES BICONDICIONALES
PROPOSICIONES NEGATIVAS
Conectivos lógicos
13 octubre 2013
PROPOSICIONES CONDICIONALES
PROPOSICIONES CONDICIONALES DIRECTAS
PROPOSICIONES CONDICIONALES INVERSAS
Conectivos lógicos
PROPOSICIONES HIPOTÉTICAS
Da clic para seguir el vínculo:
PROPOSICIONES CONDICIONALES DIRECTAS
PROPOSICIONES CONDICIONALES INVERSAS
Conectivos lógicos
FORMALIZACIÓN DE LAS PROPOSICIONES
Las proposiciones se pueden formalizar mediante el uso de símbolos para representar los diferentes elementos que se presentan dentro de la proposición compuesta, permitiendo así su fácil análisis y determinar su validez, es decir, para determinar si son verdaderos (V) o falsos (F), consta de 3 grupos, y signos auxiliares. Ver más...
VARIABLES LÓGICAS O PROPOSICIONALES
Conectivos LÓGICOS
JERARQUÍA DE CONECTORES
SIGNOS AUXILIARES
10 octubre 2013
CONECTORES LÓGICOS
CONECTIVOS LÓGICOS PARA LA DISYUNCIÓN INCLUSIVA
CONECTIVOS LÓGICOS PARA LA DISYUNCIÓN EXCLUSIVA
CONECTIVOS LÓGICOS PARA LA CONDICIONAL
CONECTIVOS LÓGICOS PARA LA BICONDICIONAL
CONECTIVOS LÓGICOS PARA LA NEGACIÓN
OPERADORES LÓGICOS
CONECTIVOS LÓGICOS PARA LA DISYUNCIÓN INCLUSIVA
CONECTIVOS LÓGICOS PARA LA DISYUNCIÓN EXCLUSIVA
CONECTIVOS LÓGICOS PARA LA CONDICIONAL
CONECTIVOS LÓGICOS PARA LA BICONDICIONAL
CONECTIVOS LÓGICOS PARA LA NEGACIÓN
CONSTANTES LÓGICAS
Son también conocidos como operadores, conectores o conectivos, son aquellos que sirven de enlace, conectan o unen 2 proposiciones para formar nuevas proposiciones compuestas, Ver más...
Da clic para seguir el vínculo:
CONECTIVOS LÓGICOS PARA LA CONJUNCIÓN
CONECTIVOS LÓGICOS PARA LA DISYUNCIÓN INCLUSIVA
CONECTIVOS LÓGICOS PARA LA DISYUNCIÓN EXCLUSIVA
CONECTIVOS LÓGICOS PARA LA CONDICIONAL
CONECTIVOS LÓGICOS PARA LA BICONDICIONAL
CONECTIVOS LÓGICOS PARA LA NEGACIÓN
TABLAS DE VERDAD
TABLAS DE LA VERDAD DE LA CONJUNCIÓN
TABLAS DE LA VERDAD DE LA DISYUNCIÓN
TABLAS DE LA VERDAD DE LA DISYUNCIÓN EXCLUSIVA (FUERTE)
TABLAS DE LA VERDAD DE LA CONDICIONAL
TABLAS DE LA VERDAD DE LA BICONDICIONAL
TABLAS DE LA VERDAD DE LA NEGACIÓN
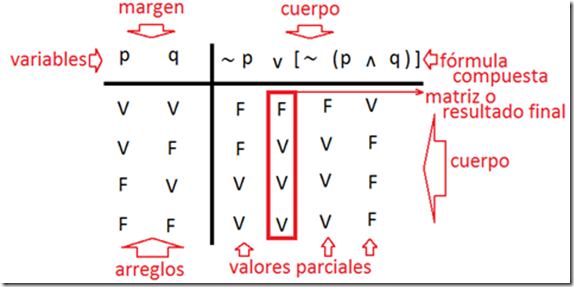
PARTES DE LA TABLA DE VERDAD
TABLAS DE LA VERDAD DE LA DISYUNCIÓN
TABLAS DE LA VERDAD DE LA DISYUNCIÓN EXCLUSIVA (FUERTE)
TABLAS DE LA VERDAD DE LA CONDICIONAL
TABLAS DE LA VERDAD DE LA BICONDICIONAL
TABLAS DE LA VERDAD DE LA NEGACIÓN
INFERENCIAS INMEDIATAS
Se entiende por Inferencias inmediatas a aquellas inferencias cuya conclusión se obtiene de una sola premisa.
Su esquema lógico es el siguiente:
INFERENCIAS MEDIATAS

VALIDEZ DE LAS INFERENCIAS.
Evaluación de una inferencia
PASOS:
Primero de deben Reconocer las premisas y su conclusión.
Reconocer los variables que forman parte de la inferencia, es decir, darles un valor simbólico (p, q, r, s, etc.).
Formalizar Premisas y Conclusiones.
Unir premisas a través de las conjuntivas y el conjunto de las premias con la conclusión a través de una condicional.
Evaluar el esquema por tabla de verdad.
Implicación Lógica
Se presenta la implicación lógica cuando una fórmula "A" se une a otra fórmula "B" a través del condicional, teniendo en cuenta que "A" el antecedente y "B" el consecuente, el resultado final de esta evaluación necesariamente debe ser una tautología; por lo tanto, se debe tener en cuenta que una implicación lógica no es lo mismo que una condicional; sólo será implicación cuando esta relación dé como resultado un esquema tautológico, ya que, si es consistente o contradictorio, se dirá que simplemente es un esquema condicional.
Equivalencia Lógica
La equivalencia lógica es una relación lógica que se presenta cuando 2 fórmulas se unen a través del bíimplícador, y que cuando son evaluadas por la tabla de verdad se obtiene como resultado una tautología;, por esto, se debe tener presente que la equivalencia lógica y la proposición bicondicional constituyen cosas muy distintas; solo se puede hablar de equivalencia sí el resultado final de la evaluación es tautológico, pero si no es tautológico se dirá que es un esquema de proposición bicondicional.
DEFINICIÓN DE LAS PROPOSICIONES CATEGÓRICAS
Las proposiciones categóricas son afirmaciones sobre las clases, de tal manera que aseveran o niegan si una clase está dentro de otra, ya sea en parte o completamente; las proposiciones categóricas tienen como características fundamentales:Ver más...
CARACTERÍSTICAS DE LAS PROPOSICIONES CATEGÓRICAS
1. Tienen sujeto y/o predicado.- Los cuales indican clases o conjuntos.Ver más...
FORMAS TÍPICAS DE LAS PROPOSICIONES CATEGÓRICAS
Se consideran 4 formas, los lógicos de la edad media les dieron las vocales: A, E, I, O; donde:
A= Todos los S son P: proposición universal afirmativa, muestra una inclusión total de “S” en “P”
E= Ningún S es P: proposición universal negativa, muestra una exclusión total de “S” en “P”
I= Algunos S son P: proposición particular afirmativa, expresa inclusión parcial de “S” en “P”
O= Algunos S no son P: proposición particular negativa, expresa exclusión parcial de “S” en “P”Ver más...
A= Todas las llamas son auquénidos.
E= Ninguna llama es auquénido.
I= Algunas llamas son auquénidos.
O= Algunas llamas no son auquénidos.
CLASIFICACIÓN DE LAS PROPOSICIONES CATEGÓRICAS
Las proposiciones categóricas se clasifican por:
1. Cantidad:
Universal.- es cuando el sujeto se refiere a todos los miembros de la clase designada, Ejemplo: todas las ovejas dan lanaVer más...
Afirmativa.- estas proposiciones afirman la inclusión total o parcial de una clase respecto de otra, Ejemplo: la pared es dura.Ver más...
Buscar en este blog
Criterio de valoración probatoria de la sospecha grave en la prisión preventiva en el delito de lavado de activos
Se ha publicado la tesis del Abg. Jonattan Poul León Segura, tesis titulada: " Criterio de valoración probatoria de la sospecha grave...