Las sucesiones literales como su nombre lo dice están formadas por órdenes lógicos de letras, dichos órdenes incluyen las reglas del alfabeto o abecedario, y ya que el abecedario varia en el uso de algunas letras se pueden especificar las siguientes reglas:
En primer lugar verificar si el orden pertenece al abecedario si es así, entonces recordar que el abecedario tiene dos tipos, el que incluye la ch y la ll y el que no las incluye, en estos casos si dentro del ejercicio o las alternativas aparece la ch o la ll entonces se deben considerar ambas dentro del abecedario, pero si no están incluidas se debe usar el abecedario que no las contiene; Si el orden no responde al abecedario significa que dichas letras corresponden al orden de palabras o la primeras letras de un orden tal como los días de la semana (l, m, m, j, V, s, d) o los meses (e, f, m, a, m , j, j, a, s, o, n, d)
En algunos casos algunos autores acostumbran a enumerar las letras del abecedario para de esta manera facilitar el desarrollo de estos ejercicios.
Ver más...
Ejercicios:
Caso 1
Que letra continúa la sucesión:
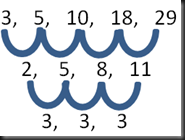
A,e,h,…
En este caso observamos como la variación es de:

Por tanto la letra siguiente es la “j”
Ver más...
Caso 2
Que letra es la que sigue en la siguiente sucesión:
s, o, r, b, i,…
En este caso podemos observar que la ley de formación esta determinada por la palabra libros pero invertida, por tanto la letra faltante es la “L”
Ver más...
Caso 3
Que letra continúa la sucesión:
d, l, m,…
En este caso se refiere a los días de la semana empezando por el domingo, por tanto la letra que sigue es la “m” de miércoles.
Ver más...
Da clic para seguir el vínculo:
La sucesión