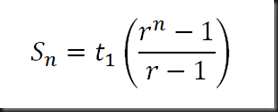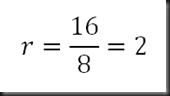Busca tu tema aquí - Google - Lizerindex®
18 marzo 2015
Las Matemáticas en la Cultura Caldeo - Asiria
24 julio 2012
FUNCIONES DE UNA VARIABLE
Función
Es una regla que denota que un elemento de un conjunto es correspondiente a otro único elemento de otro conjunto.
Ejm:
(1,4); (2,4); (3,4)
Da clic para seguir el vínculo:
19 julio 2012
UTILIDAD
Es la ganancia neta de la empresa, es decir lo que queda del ingreso al definir los costos, su representación matemática es:
Ejercicios:
INGRESO
Es la entrada de capitales de una empresa producto de la venta de su producción sin definir los costos, está en función del precio y la cantidad producida, su representación matemática es:
Ejercicios de Costos
a) Encuentra la ecuación de costo lineal y grafique.
b) Determine el costo de producir 6000 kilogramos de azúcar en un día y diarios por una semana.
Desarrollo:
a) Para hallar la ecuación de costo ordenamos datos:
0,59 x + 5000
b) Por producir 6000 kilogramos:

Por producir 6000 diarios por una semana:

Ver más...
a) La relación entre el costo total de producir “X” celulares al día y gráfica.
b) ¿Cuántos celulares se pueden producir con $ 30000000?
Desarrollo:
a) Primero simulamos las funciones de costo teniendo en cuenta los siguientes datos:
Función de costos 1:
CT= 12500000
X= 25000
Función de costos 2:
CT = 47000000
X = 100000
Recordar que ambas funciones de costos pertenecen a una sola, es decir:
Ahora ordenamos datos:

Ahora para hallar el costo fijo reemplazamos en la ecuación el valor del costo variable:
25000 (460) + B = 12500000
11500000 + B = 12500000
B = 1000000
La ecuación de costos queda de la siguiente manera:
CT = 460 X + 1000000
b) Para hallar la cantidad de celulares que se pueden producir igualamos la cantidad de dinero con la ecuación de costo total:
30000000 = 460 X + 1000000
29000000 = 460 X
X = 63043,48
Se pueden producir 63043 celulares con $ 30000000
Ver más...
ANÁLISIS DE PUNTO DE EQUILIBRIO

Ver más...
En una fábrica de vehículos el costo de mano de obra y de los materiales por auto es de S/. 60000 y los costos fijos son de S/. 15000000 al día( si se vende cada reloj en S/. 150000), ¿Cuántos autos debe producir y vender a diario con el objeto de garantizar que el negocio no tenga ganancias ni pérdidas?
Desarrollo:
Primero hallamos la función de costos:
60000 X + 15000000
Luego hallamos la función de ingreso:
150000 x
Luego igualamos las formulas y hallamos el equilibrio:
60000 X + 15000000 = 150000 X
15000000 = 150000 X - 60000 X
15000000 = 90000 X
166,67 = X
Se deben producir 166 carros para no perder ni ganar.
Ver más...
Limites
En un punto dado en el plano existe lo que se llama limite de una función y siempre que este en el dominio de dicha función para todo tiene que ser mayor que cero S>0 E>0
Si: Lim fx=L /f(x) - L/ < E siempre que (sq´) (X – X0/ < S X → X0
Ejemplo:
Determinar “S” en términos de “E”
1) Lim ( 7X + 2) = 37 ; S = F (E) X → 5
Desarrollo:
/7X+2-37/<E sq´ /X-5/<S
/7X-35/<E sq´ /X-5/<S
7/X-5/< E sq´ /X-5/<S
/X-5/< E/7 sq´ /X-5/<S
S = E / 7
2) Lim (X2-3X+4) = 8 X→4
Desarrollo:
/X2-3X+4-8/<E sq´ /X-4/<S
/X2-3X-4/<E sq´ /X-4/<S
/X+1/ /X-4/<E sq´ /X-4/<S
Entonces:
-1< X -4 < 1
3 < X < 5
Por X+1 se le suma a cada extremo:
4 < X < 6
Y se obtiene:
4 < X-4 < 6
-6 < X-4 < 6
/X-4/< 6
E= {1, E/6}
3) Lim (X3+2X2-3X+1)=11 X→2
Desarrollo:
/X3+2X2-3X+1-11/<E sq´ /X – 2/ < S
/X3+2X2-3X-10/<E sq´ /X – 2/ < S
/X-2/ /X2+4X+5/ <E sq´ /X-2/ <S
Entonces:
-1 < X-2 < 1
1 < X < 3
(1)2 < (X)2 < (3)2
1 < X2 < 9
Tal que:
9 < 4X +5 < 17
Sumamos ambas cantidades:
10 < X2+4X+5 < 26
-26 < X2+4X+5 < 26
/X2+4X+5/ < 26
S = { 1 , E/26}
DOMINIO Y RANGO DE UNA FUNCIÓN
1. Forma simbólica.- los primeros elementos de un par ordenado son considerados el dominio y los elementos segundos son el rango.
2. Forma gráfica.- observar el dominio en el eje “X” y el rango en el eje “Y”
3. Forma analítica.- para hallar el dominio primero debemos despejar la variable en el eje “Y”; para hallar el rango la variable “X” debe despejarse; y debemos considerar:

Ver más...
Hallar el dominio en:

- En primer lugar como lo que debemos hallar es el dominio entonces debemos despejar la “y”, en este caso ya está despejada.
Ahora consideramos la primera opción dada en la forma analítica:

Ahora lo ubicamos en la gráfica:

Y obtenemos como resultado:

Ver más...
Intervalos
GRÁFICA DE FUNCIONES
1. El dominio de la función
2. Intercepción de los ejes “X” e “Y”
3. Asíntotas
4. Tabulación
5. Gráfica
Ejm:
Graficar la siguiente función:

Ver más...
Df= 10= 0 ; X-2 = 0 X= 2 ; por lo tanto el dominio de la función esta determinado por:
Luego hallamos los puntos de intercepción con el eje “x” e “y”
Reemplazamos el cero en las variables:

Por tanto la curva se cruza con el eje “y” en ese punto.
Ahora tomar en cuenta las asíntotas:
Para ello se debe despejar la “Y” para la asíntota vertical y luego la “X” para la asíntota horizontal:
Asíntota vertical:
Como “y” ya está despejada, lo único que hacemos es igualar el denominador a cero para obtener el valor de “X”

La asíntota se da en el número dos, es decir el resultado es indeterminado o infinito
Asíntota horizontal:
Debemos despejar la “X”:

Ahora igualamos a cero el denominador de la ecuación:
y = 0
La asíntota se da en el número cero, es decir el resultado es indeterminado o infinito
Ver más...

Ver más...
14 julio 2012
Sucesión alternada o mesclada

Ver más...
Ejercicios de sucesión alternada o mesclada
Progresión aritmética
Progresión geométrica
La sucesión
Sucesiones literales
Caso 1
Que letra continúa la sucesión:
A,e,h,…
En este caso observamos como la variación es de:

Por tanto la letra siguiente es la “j”
Ver más...
Que letra es la que sigue en la siguiente sucesión:
s, o, r, b, i,…
En este caso podemos observar que la ley de formación esta determinada por la palabra libros pero invertida, por tanto la letra faltante es la “L”
Ver más...
Que letra continúa la sucesión:
d, l, m,…
En este caso se refiere a los días de la semana empezando por el domingo, por tanto la letra que sigue es la “m” de miércoles.
Ver más...
La sucesión
Ejercicios de sucesión alternada o mesclada
2, 3, 6, 7, 18, 11,…
Para resolver este ejercicio debemos tener en cuenta la ley de formación de las dos sucesiones que están mescladas en esta sucesión, luego para números impares o pares se usan estas fórmulas individuales:
Para números pares:
Si te piden un número par este será otro número en la progresión individual, por ello se usa esta fórmula:
Para números impares:
Si te piden un número par este será otro número en la progresión individual, por ello se usa esta fórmula:
Ahora mostremos gráficamente la ley de formación de esta sucesión:
2, 3, 6, 7, 18, 11,…

Para hallar el término 10 detectamos que es un número par entonces:
10 = 2 n n=5 y su razón de los números pares es +4 (progresión aritmética)

El termino 10 de la sucesión es 19
Para hallar el término 11 detectamos que es un número impar entonces:
11= 2n-1 n=6 y su razón de los números pares es ×3 (progresión geométrica)

El termino 11 de la sucesión es 486
Da clic para seguir el vínculo:
Progresión aritmética
Progresión geométrica
La sucesión
Sucesión combinada o mixta
2, 6, 8, 24,…
Para hallar el 5 y 6 término se procede de la siguiente manera:
La sucesión tiene la siguiente ley de formación:

Por tanto el 5to término es: 24 + 2 = 26
y el 6to termino es: 26 X 3 = 78
Ver más...
4, 8, 40, 320,…
Hallar el 5 y 6 término se procede de la siguiente manera:
En este caso la ley de formación está dada así:
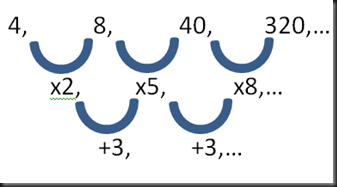
Por tanto el 5to término es: (8 + 3) x 320 =3520
y el 6to termino es: (11 + 3) x 3520 = 49280
Ver más...
La sucesión
La serie
Es decir si la sucesión fuera de esta manera se realiza lo siguiente:
Hallar la serie de la siguiente sucesión de números:
Da clic para seguir el vínculo:
Sucesión aritmética
Sucesión geométrica
Sucesión combinada o mixta
Sucesión alternada
Sucesiones literales
Sucesiones alfanuméricas
Sucesiones especiales numéricas
La sucesión
Hallar la sumatoria de términos de una progresión geométrica.
Dónde:
Sn=suma de términos
t1=primer término
r=razón
n=número de términos
Ver más...
De la siguiente progresión geométrica halla la suma de los 20 primeros términos:
3, 9, 27, 81, …
Primero hallamos la razón:
Ahora aplicamos la fórmula:
Ver más...
Hallar el enésimo término de una progresión geométrica.
Sucesión alternada o mesclada
La sucesión
Hallar el enésimo término de una progresión geométrica.

Dónde:
tn=término enésimo
t1=primer término
r=razón
n=número de términos
Ver más...
Ejemplo:
De la siguiente progresión geométrica hallar el termino 20vo
3, 9, 27, 81, …
Primero hallamos la razón:

Ahora aplicamos la fórmula:

Ver más...
Da clic para seguir el vínculo:
Hallar la sumatoria de términos de una progresión geométrica.
Sucesión alternada o mesclada
La sucesión
Progresión Geométrica
Dónde:
t1= primer término.
t2= segundo término.
tn= último término.
a= razón (es igual para toda la ley de formación y se resuelve multiplicando)
La fórmula para hallar la razón se puede usar de la siguiente forma:
Dónde:
tn= término enésimo
tn-1= término anterior al término enésimo
Ver más...
De la siguiente progresión geométrica hallar la razón:
2, 4, 8, 16, …
Por formula:
Ver más...
Hallar el enésimo término de una progresión geométrica.
Hallar la sumatoria de términos de una progresión geométrica.
Sucesión alternada o mesclada
La sucesión
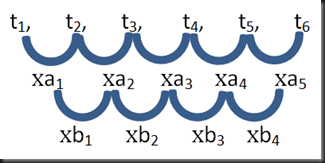
Sucesión Geométrica
Es aquella en la cual la ley de formación esta dada por el operador de la multiplicación, es decir:
Dónde:
t1= primer término.
a1=primera fila de razones
b2= segunda fila de razones
Ver más...
Ver más...
Progresión geométrica
Sucesión alternada o mesclada
La sucesión
Suma de términos de una Progresión Aritmética

Dónde:
t1= primer término.
tn= último término.
r= razón
n= número de términos
Sn=suma de términos
Ver más...
De la siguiente progresión aritmética
3, 5, 7, 9, 11…
Hallar la suma de los cinco y de los veinte primeros términos de la progresión aritmética

Para hallar el término veinte
Aplicamos la fórmula para hallar el término enésimo:
t20 = 3 + 2 (20 - 1) = 41
Ahora hallamos la suma:
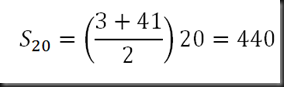
Ver más...
Término enésimo de una progresión aritmética
Sucesión alternada o mesclada
La sucesión
Término enésimo de una Progresión Aritmética

Dónde:
t1= primer término.
tn= último término.
r= razón
n= número de términos
Ver más...
De la siguiente sucesión:
3, 5, 7, 9, 11…
Hallar el término 6 y el 20
t6 = 3 + 2 (6 - 1) = 13
t20 = 3 + 2 (20 - 1) = 41
Ver más...
Suma de términos de una Progresión Aritmética
Sucesión alternada o mesclada
La sucesión
Buscar en este blog
Criterio de valoración probatoria de la sospecha grave en la prisión preventiva en el delito de lavado de activos
Se ha publicado la tesis del Abg. Jonattan Poul León Segura, tesis titulada: " Criterio de valoración probatoria de la sospecha grave...