Con Colombia
Busca tu tema aquí - Google - Lizerindex®
03 diciembre 2013
TRATADOS LIMÍTROFES DEL PERÚ
Con Colombia
02 diciembre 2013
El Fin del Poder Judicial Peruano
28 noviembre 2013
Amor a los Andes
Bienvenid@
“Amor a los Andes” es el primer libro publicado de Jonattan Poul León Segura, mediante el servicio de Amazon.com, cuenta la historia de un amor en contra de la voluntad, todos los hechos se desarrollan en un pueblecillo en las alturas de la cordillera de los andes, si quieres ver una versión previa del libro da clic en el siguiente enlace:
Vista Previa de “AMOR A LOS ANDES”
o también puedes dar clic en las imágenes a continuación:
Aprovecha esta promoción al inmejorable precio de $ 1.00 (USD), te invito a descubrir “Amor a los Andes”
Para ver contenido gratuito del autor, estas invitad@ a: Amor Apasionado
26 noviembre 2013
LÓGICA
Etimológicamente la palabra Lógica proviene del término griego: LOGIKE que significa “tratado, idea o pensamiento”
Por lo tanto la palabra Lógica se puede definir como “el tratado del pensamiento desde el punto de vista formal”.
Da clic para seguir el vínculo:
ETIMOLOGÍA DE LA LÓGICA
Etimológicamente la palabra Lógica proviene del término griego: LOGIKE que significa “tratado, idea o pensamiento”
Por lo tanto la palabra Lógica se puede definir como “el tratado del pensamiento desde el punto de vista formal”.
Ver más...
DEFINICIÓN DE LA LÓGICA
HISTORIA DE LA LÓGICA
EL LENGUAJE
LAS FALACIAS
LAS PROPOSICIONES
TABLAS DE VERDAD
LA INFERENCIA
LAS PROPOSICIONES CATEGÓRICAS
CUADRO DE BOECIO
TERMINOS DISTRIBUIDOS
SILOGISMO CATEGÓRICO
DEFINICIÓN DE LA LÓGICA
La lógica es considerada en el grupo de las ciencias formales, cuya rama de estudio es la estructura de los conceptos, juicios y raciocinios sus relaciones, sus condiciones de validez y sus leyes. Por lo tanto, se puede decir que la lógica es “La Teoría de la Inferencia”.
Da clic para seguir el vínculo:
ETIMOLOGÍA DE LA LÓGICA
HISTORIA DE LA LÓGICA
EL LENGUAJE
LAS FALACIAS
LAS PROPOSICIONES
TABLAS DE VERDAD
LA INFERENCIA
LAS PROPOSICIONES CATEGÓRICAS
CUADRO DE BOECIO
TERMINOS DISTRIBUIDOS
SILOGISMO CATEGÓRICO
HISTORIA DE LA LÓGICA
Da clic para seguir el vínculo:
ORIGEN DE LA LÓGICA
EDAD ANTIGUA
EDAD MEDIA
EDAD MODERNA
EDAD CONTEMPORÁNEA
ORIGEN DE LA LÓGICA
La Lógica tiene sus inicios en Grecia con los primeros pensadores del período cosmológico o presocrático y se desarrolla a la par de la Filosofía. Aristóteles gracias a sus aportes en esta ciencia es considerado como “Padre de la Lógica”
EDAD ANTIGUA
EDAD MEDIA
EDAD MODERNA
EDAD CONTEMPORÁNEA
LENGUAJE Y LA LÓGICA
La Lógica es una disciplina que se dedica al proceso de razonamiento de los individuos, deja el estudio del lenguaje al margen de sus estudios. Está muy claro que la lógica no pretende estudiar el lenguaje, a esta rama de la ciencia se dedica la Lingüística. Sin embargo, los razonamientos que interesan a la lógica son aquellos que se han producido ya, para saber si se han dado de manera válida o no. Y ello sería imposible conseguir sin tener un medio de comprensión tal como el lenguaje, los razonamientos son expresados y comunicados a través del uso de un lenguaje determinado. En otras palabras, la lógica estudia la validez de los razonamientos, y los expresa lingüísticamente. Si no se tiene presente las funciones y los usos del lenguaje, sería imposible o erróneo el análisis de los razonamientos. utilizando el lenguaje se podría presentar un razonamiento no válido como si lo fuera. Por ello es que le interesa a la lógica tener presente y con claridad las funciones y los usos del lenguaje.
Da clic para seguir el vínculo:
DEFINICIÓN DEL LENGUAJE LÓGICO
Es un sistema de símbolos y signos, que tienen un conjunto de reglas creadas por el hombre con la intensión de comunicarse.
El lenguaje como medio de comunicación, tiene diferentes funciones; ya sea para informar, deleitar o persuadir, de tal manera que podamos diferenciar la clase de discurso que llevamos a cabo, examinando la función que está desempeñando el lenguaje del que hacemos uso.
FUNCIONES BÁSICAS DEL LENGUAJE
FALACIAS
DEFINICIÓN.
Es un razonamiento que aparenta ser válido; se puede decir que es muy convincente, pero cuando es sometido a un análisis cuidadoso, y sin tener en cuenta las emociones que nos produzca o intente producir en nosotros, resulta no ser válido.
Da clic para seguir el vínculo:
CLASES DE FALACIAS
Da clic para seguir el vínculo:
FALACIAS FORMALES
FALACIAS NO FORMALES
También puedes dar clic para saber acerca de:
SILOGISMOS
FALACIAS FORMALES
se cometen cuando se elabora un razonamiento infringiendo las reglas lógicas de la deducción, que le dan validez. Ejemplo:
La falacia de cuaternio terminorum (cuarto término).
Estas falacias son tratadas dentro del estudio de los silogismos.
Da clic para seguir el vínculo:
FALACIAS NO FORMALES
FALACIAS DE ATINGENCIA
FALACIAS DE AMBIGÜEDAD
LA INFERENCIA
Se define como el paso de un conjunto de premisas a una conclusión. Dichas premisas y las conclusiones están compuestas por proposiciones, la inferencia puede considerarse como una estructura de proposiciones, estas proposiciones adquieren el nombre de premisas con el fin de obtener otra proposición mayor llamada conclusión. Una inferencia tiene la forma de un esquema molecular condicional o proposición condicional, es decir, el símbolo principal es el condicional (→), cuyo antecedente es la premisa o premisas unidas por conjunciones y cuyo consecuente es la conclusión.
En las inferencias se puede observar que las premisas de la conclusión se manifiestan después de uso de palabras como: por lo tanto, luego, en conclusión, en consecuencia, ergo, etc.
Da clic para seguir el vínculo:
DEFINICIÓN DE LA INFERENCIA
Se define como el paso de un conjunto de premisas a una conclusión. Dichas premisas y las conclusiones están compuestas por proposiciones, la inferencia puede considerarse como una estructura de proposiciones, estas proposiciones adquieren el nombre de premisas con el fin de obtener otra proposición mayor llamada conclusión. Una inferencia tiene la forma de un esquema molecular condicional o proposición condicional, es decir, el símbolo principal es el condicional (→), cuyo antecedente es la premisa o premisas unidas por conjunciones y cuyo consecuente es la conclusión.
En las inferencias se puede observar que las premisas de la conclusión se manifiestan después de uso de palabras como: por lo tanto, luego, en conclusión, en consecuencia, ergo, etc.
Da clic para seguir el vínculo:
25 noviembre 2013
CLASES DE INFERENCIAS
Las inferencias se pueden clasificar de dos formas:
Da clic para seguir el vínculo:
LAS PROPOSICIONES CATEGÓRICAS
Las proposiciones categóricas son afirmaciones sobre las clases, de tal manera que aseveran o niegan si una clase está dentro de otra, ya sea en parte o completamente; las proposiciones categóricas tienen como características fundamentales:
1. Tienen sujeto y/o predicado.- Los cuales indican clases o conjuntos.Ver más...
Da clic para seguir el vínculo:
FORMAS TÍPICAS DE LAS PROPOSICIONES CATEGÓRICAS
SILOGISMO
Es una inferencia deductiva mediata, conformada por tres proposiciones categóricas, las dos primeras se llaman premisas y la última se llama conclusión.Ver más...
Ninguna madera es quebradiza (Premisa mayor)
Alguna madera esta picada (Premisa menor)
Por lo tanto. Algunas picadas no son quebradizas (Conclusión)
Da clic para seguir el vínculo:
Estructura formal del silogismo
Reglas del silogismo
Figuras del silogismo
Modos del silogismo
Modos validos del silogismo
Forma del silogismo categórico
Prueba de validez del silogismo y uso del diagrama de Venn
CUADRO DE BOECIO
Es también conocido como el CUADRO DE LA OPOSICIÓN, muestra los relaciones de las proposiciones categóricas típicas (A, E, I, O) entre sí. Estas relaciones son llamadas: contradictorias, contrarias, subcontrarias, subalternas y subalternantes. Ver más...
Se puede graficar de la siguiente manera:
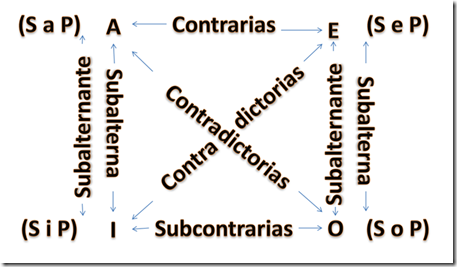
Da clic para seguir el vínculo:
Proposiciones contrarias
Proposiciones subcontrarias
Proposiciones subalternas
Proposiciones contradictorias
Proposiciones subalternantes
CUADRO DE LA OPOSICIÓN
Es también conocido como el CUADRO DE BOECIO, muestra los relaciones de las proposiciones categóricas típicas (A, E, I, O) entre sí. Estas relaciones son llamadas: contradictorias, contrarias, subcontrarias, subalternas y subalternantes. Ver más...

Da clic para seguir el vínculo:
Proposiciones contrarias
Proposiciones subcontrarias
Proposiciones subalternas
Proposiciones contradictorias
Proposiciones subalternantes
DEFINICION DEL SILOGISMO CATEGÓRICO
El silogismo fue usado por primera vez en la antigüedad por Aristóteles.
Es una inferencia deductiva mediata, conformada por tres proposiciones categóricas, las dos primeras se llaman premisas y la última se llama conclusión.Ver más...
Ninguna madera es quebradiza (Premisa mayor)
Alguna madera esta picada (Premisa menor)
Por lo tanto. Algunas picadas no son quebradizas (Conclusión)
Estructura formal del silogismo
Reglas del silogismo
Figuras del silogismo
Modos del silogismo
Modos validos del silogismo
Forma del silogismo categórico
Prueba de validez del silogismo y uso del diagrama de Venn
SILOGISMO CATEGÓRICO
El silogismo fue usado por primera vez en la antigüedad por Aristóteles.
Es una inferencia deductiva mediata, conformada por tres proposiciones categóricas, las dos primeras se llaman premisas y la última se llama conclusión.Ver más...
Ninguna madera es quebradiza (Premisa mayor)
Alguna madera esta picada (Premisa menor)
Por lo tanto. Algunos madera picada no es quebradiza (Conclusión)
Estructura formal del silogismo
Reglas del silogismo
Figuras del silogismo
Modos del silogismo
Modos validos del silogismo
Forma del silogismo categórico
Prueba de validez del silogismo y uso del diagrama de Venn
21 noviembre 2013
CUATERNIO TERMINORUM
Conocida como Cuarto Termino, esta falacia se comete cuando el término medio del silogismo es ambiguo, por lo cual, puede tener un doble significado, esto produce que el término medio se duplique. Ver más...
Ejemplo:
Lima es una ciudad superpoblada (ciudad: Lima)
Alguna lima está muy madura (fruta: lima)
Alguna madura esta superpoblada (falacia)
Falacias Formales en los silogismos
Mayor ilícito
Esta falacia se presenta cuando dentro del silogismo, el término mayor tiene en la conclusión la premisa mayor.Ver más...
Todo carpintero usa martillo
Ningún nadador usa martillo
Ningún nadador es carpintero (falacia)
Falacias Formales en los silogismos
Forzado o ilícito
Cuando de dos premisas afirmativas, se infiere una conclusión negativa.
Ejemplo:
Todo matemático es estudioso
Algunos alumnos son matemáticos
Ningún alumno es estudioso (falacia)
Da clic para seguir el vinculo:
Medio concluyente
Esta falacia se presenta cuando el término medio está presente dentro de la conclusión.
Los perros son mamíferos
Los gatos son mamíferos
Todo gato es mamífero (falacia)
Falacias Formales en los silogismos
Falacia de las premisas excluyentes
Cuando de dos premisas negativas se llega a una conclusión.
Ningún periodista es discreto
Algunos profesionales no son periodistas
Algunos profesionales no son discretos (falacia)
Falacias Formales en los silogismos
Medio ilícito
Esta falacia ocurre cuando el término medio no tiene en ninguna de las premisas cantidad universal.
Algún perro es un amigo
Toda perro es un animal
Todo animal es un amigo (falacia)
Falacias Formales en los silogismos
Menor ilícito
Cuando el término menor tiene en la conclusión mayor cantidad (cantidad universal) que en las premisas.
Todas las mesas son de madera
Todas las sillas son de madera
Todas las sillas son mesas (falacia)
Falacias Formales en los silogismos
CUARTO TÉRMINO
conocida también como “cuaternio terminorum” esta falacia se comete cuando el término medio del silogismo es ambiguo, por lo cual, puede tener un doble significado, esto produce que el término medio se duplique.
Lima es una ciudad superpoblada (ciudad: Lima)
Alguna lima está muy madura (fruta: lima)
Alguna madura esta superpoblada (falacia)
Falacias Formales en los silogismos
TERCERA FIGURA DEL SILOGISMO
El término medio es sujeto en ambas premisas. Así: Todos los jóvenes son la esperanza del Perú Algunos jóvenes son estudiantes Luego, Algunos estudiantes son la esperanza del Perú
M P Todos los equipos de sonido tienen volumen
M S algunos equipos de sonido tienen reproductores de CD
S P luego, algunos reproductores de CD tienen volumen
FIGURAS DEL SILOGISMO
SEGUNDA FIGURA DEL SILOGISMO
El término medio es predicado en ambas premisas. Ejemplo:
P M todo clavo es de hierro
S M ningún lápiz es de hierro
S P luego, ningún lápiz es un clavo
FIGURAS DEL SILOGISMO
PRIMERA FIGURA DEL SILOGISMO
El término medio es sujeto de la premisa mayor y predicado de la premisa menor. Así:
M P toda ropa es lavable
S M todo pantalón es ropa
S P luego, todo pantalón es lavable
FIGURAS DEL SILOGISMO
CUARTA FIGURA DEL SILOGISMO
El término medio es predicado de la premisa mayor y sujeto de la premiso menor. Ejemplo:
P M Ningún perro es gato
M S Algunos gatos son animales nocturnos
S P Algunos animales nocturnos no son perros
FIGURAS DEL SILOGISMO
Proposiciones Contrarias
Se les llama proposiciones contrarias porque son idénticas en cantidad, pero diferentes en calidad: A-E.
De la verdad de una contraria, se infiere la falsedad de la otra; no pueden ser simultáneamente verdaderas pero sí simultáneamente falsas. Ejemplo:
A: Toda llama es auquénido
E: Ninguna llama es auquénido
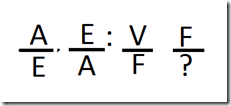
Proposiciones Subcontrarias
Son idénticas en cantidad, pero diferentes en calidad: I - O.
De la falsedad de una subcontraria se infiere la verdad de la otra pero no viceversa; Pueden ser simultáneamente verdaderas, pero no simultáneamente falsas.
I: Algún auquénido es llama
O: Algún auquénido no es llama

Proposiciones Subalternas
Son diferentes en cantidad, pero similares en calidad: A-I, E - O.
De la verdad de la universal se infiere la verdad de la particular pero no viceversa; es decir, pueden ser en algún caso simultáneamente verdaderas.
De toda llama es auquénido (verdadera) se infiere la verdad de la particular Alguna llama es auquénido (verdadera) Esquemáticamente se tiene:

Proposiciones Contradictorias
Son diferentes en cantidad y calidad: A-O, E -I.
De la verdad de una contradictoria, se infiere la falsedad de otra y viceversa.
O: Algún auquénido es llama
A: Todo auquénido es llama
Ejemplo 2:
E: Ningún estudioso saca malas calificaciones
I: Algún estudioso saca malas calificaciones.
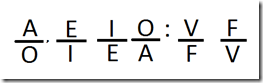
Proposiciones Subalternantes
Cada proposición universal es subalternante de su particular I-A; O-E.
De la falsedad de la particular se infiere la falsedad de la universal pero no viceversa, por lo tanto ambas pueden ser falsas.
De alguna madera es metal (falsa) se infiere la falsedad de la universal Toda madera es metal (falsa) Esquemáticamente se tiene:

TÉRMINOS DISTRIBUIDOS
Un término está distribuido en una proposición categórica típica cuando aparece en toda su extensión.
A: Todo S es P El término distribuido hace las veces de SUJETO.
E: Ningún S es P Los términos distribuidos son el SUJETO Y el PREDICADO.
I: Algún S es P NO TIENE TÉRMINO DISTRIBUIDO.
O: Algún S no es P El término distribuido hace las veces de PREDICADO.
A; todas las llamas son auquénidos
E: Ninguna madera es metal
O: Algunos abogados son empresarios
ESTRUCTURA FORMAL DEL SILOGISMO
Premisa Mayor.- (PM) Es la que contiene al término mayor y al término medio.
Premisa Menor.- (Pm) Es la que contiene al término menor y al término medio.
Conclusión.- (C) Es la respuesta lógica que proviene lógicamente de la premisa mayor y de la premisa menor. y se distingue de las proposiciones categóricas anteriores por contener sólo el término menor y el término mayor.
CLASES DEL SILOGISMO
En la composición formal del silogismo categórico también se pueden distinguir clases a las cuales se les da el nombre de "términos", siendo los siguientes:
A. Término Mayor (P).- Esta clase es la que cumple siempre la función de ser predicado en la conclusión, y, esta contenida dentro de la premisa mayor, ya sea como sujeto o predicado.Ver más...
Alguna madera esta picada (Premisa menor) Algún M es P
Por lo tanto. Algunas picadas no son quebradizas (Conclusión) Algún P no es Q
Término Mayor P quebradiza (Q)
Término Medio M madera (M)
Término Menor S picadas (P)
TERMINOS DEL SILOGISMO
En la composición formal del silogismo categórico también se pueden distinguir clases a las cuales se les da el nombre de "términos", siendo los siguientes:
A. Término Mayor (P).- Esta clase es la que cumple siempre la función de ser predicado en la conclusión, y, esta contenida dentro de la premisa mayor, ya sea como sujeto o predicado.Ver más...
Alguna madera esta picada (Premisa menor) Algún M es P
Por lo tanto. Algunas picadas no son quebradizas (Conclusión) Algún P no es Q
Término Mayor P quebradiza (Q)
Término Medio M madera (M)
Término Menor S picadas (P)
Ver más...
REGLAS DEL SILOGISMO
Reglas de los Términos
1. los silogismos esta compuesto de tres términos: menor, mayor y medio.
2. El término medio no debe estar presente en la conclusión.
3. El término medio debe estar distribuido por lo menos en una de las premisas.
4. Un término distribuido en la conclusión, debe también estar contenido en la premisa.
Ninguna madera es quebradiza (Premisa mayor)
Alguna madera esta picada (Premisa menor)
Por lo tanto. Algunas picadas no son quebradizas (Conclusión)
* PRIMERA LEY: Contiene los términos: quebradiza (mayor), Madera (medio), picada (menor)
* SEGUNDA LEY: El término medio "madera" no está presente en la conclusión
* TERCERA LEY: Madera, como término medio se encuentra contenido en la primera premisa
* CUARTA LEY: En la conclusión, el término mayor "quebradiza" está contenido y tambien se encuentra presente en la premisa mayor
Ver más...
1. De dos proposiciones afirmativas se obtiene como resultado una conclusión afirmativa. Por ejemplo:
Todos los libros son educadores (es afirmativa)
Todas las enciclopedias son libros (es afirmativa)
Luego, Todas las enciclopedias son educadores (conclusión afirmativa)
Todo metal es maleable (es afirmativa)
Ningún cristal es metal (es negativa)
Luego, Ningún cristal es maleable (conclusión negativa)
Algunos trabajadores son carpinteros
Algunos albañiles son trabajadores
Reglas de las Proposiciones
1. De dos proposiciones afirmativas se obtiene como resultado una conclusión afirmativa. Por ejemplo:
Todos los libros son educadores (es afirmativa)
Todas las enciclopedias son libros (es afirmativa)
Luego, Todas las enciclopedias son educadores (conclusión afirmativa)
2. La conclusión siempre es influenciada por la premisa más débil. Para esto, la premisa particular es más débil que la universal, y la negativa es más débil que la afirmativa. Por ejemplo:
Todo metal es maleable (es afirmativa)
Ningún cristal es metal (es negativa)
Luego, Ningún cristal es maleable (conclusión negativa)
3. De dos premisas particulares no se obtiene ninguna conclusión. Así por ejemplo:
Algunos trabajadores son carpinteros
Algunos albañiles son trabajadores
Luego, (nada se concluye)
4. Si las dos premisas son negativas no se obtiene conclusión. Por ejemplo:
Ningúna foca es reptil
Algun reptil no es de tierra
Luego, (nada se concluye)
Reglas de los Términos de los Silogismos
1. los silogismos esta compuesto de tres términos: menor, mayor y medio.
2. El término medio no debe estar presente en la conclusión.
3. El término medio debe estar distribuido por lo menos en una de las premisas.
4. Un término distribuido en la conclusión, debe también estar contenido en la premisa.
Ninguna madera es quebradiza (Premisa mayor)
Alguna madera esta picada (Premisa menor)
Por lo tanto. Algunas picadas no son quebradizas (Conclusión)
* PRIMERA LEY: Contiene los términos: quebradiza (mayor), Madera (medio), picada (menor)
* SEGUNDA LEY: El término medio "madera" no está presente en la conclusión
* TERCERA LEY: Madera, como término medio se encuentra contenido en la primera premisa
* CUARTA LEY: En la conclusión, el término mayor "quebradiza" está contenido y tambien se encuentra presente en la premisa mayor
Reglas de las Proposiciones en los Silogismos
Todos los libros son educadores (es afirmativa)
Todas las enciclopedias son libros (es afirmativa)
Luego, Todas las enciclopedias son educadores (conclusión afirmativa)
Ver más...
Todo metal es maleable (es afirmativa)
Ningún cristal es metal (es negativa)
Luego, Ningún cristal es maleable (conclusión negativa)
Ver más...
Algunos trabajadores son carpinteros
Algunos albañiles son trabajadores
Luego, (nada se concluye)
Ver más...
Ningúna foca es reptil
Algun reptil no es de tierra
Luego, (nada se concluye)
FALACIAS FORMALES EN LOS SILOGISMOS
Se presentan cuando se infringen las leyes lógicas tanto de términos como de las proposiciones en el silogismo, dichas falacias son:
CUARTO TÉRMINO:
(cuaternio terminorum) esta falacia se comete cuando el término medio del silogismo es ambiguo, por lo cual, puede tener un doble significado, esto produce que el término medio se duplique. Ejemplo:
Lima es una ciudad superpoblada (ciudad: Lima)
Alguna lima está muy madura (fruta: lima)
Alguna madura esta superpoblada (falacia)
Esta falacia se presenta cuando el término medio está presente dentro de la conclusión
Ejemplo:
Los perros son mamíferos
Los gatos son mamíferos
Todo gato es mamífero (falacia)
Esta falacia se presenta cuando dentro del silogismo, el término mayor tiene en la conclusión la premisa mayor
Ejemplo:
Todo carpintero usa martillo
Ningún nadador usa martillo
Ningún nadador es carpintero (falacia)
Esta falacia ocurre cuando el término medio no tiene en ninguna de las premisas cantidad universal.
Ejemplo:
Algún perro es un amigo
Toda perro es un animal
Todo animal es un amigo (falacia)
Cuando el término menor tiene en la conclusión mayor cantidad (cantidad universal) que en las premisas. Ejemplo:
Todas las mesas son de madera
Todas las sillas son de madera
Todas las sillas son mesas (falacia)
Cuando de dos premisas afirmativas, se infiere una conclusión negativa.
Ejemplo:
Todo matemático es estudioso
Algunos alumnos son matemáticos
Ningún alumno es estudioso (falacia)
Cuando de dos premisas negativas se llega a una conclusión.
Ejemplo:
Ningún periodista es discreto
Algunos profesionales no son periodistas
Algunos profesionales no son discretos
FIGURAS DEL SILOGISMO
Las figuras del Silogismo dependen de la colocación del término medio en las respectivas premisas. Estas figuras son cuatro:
PRIMERA FIGURA.- El término medio es sujeto de la premisa mayor y predicado de la premisa menor. Así:
M P toda ropa es lavable
S M todo pantalón es ropa
S P luego, todo pantalón es lavable
P M todo clavo es de hierro
S M ningún lápiz es de hierro
S P luego, ningún lápiz es un clavo
M P Todos los equipos de sonido tienen volumen
M S algunos equipos de sonido tienen reproductores de CD
S P luego, algunos reproductores de CD tienen volumen
P M Ningún perro es gato
M S Algunos gatos son animales nocturnos
S P Algunos animales nocturnos no son perros
Buscar en este blog
Criterio de valoración probatoria de la sospecha grave en la prisión preventiva en el delito de lavado de activos
Se ha publicado la tesis del Abg. Jonattan Poul León Segura, tesis titulada: " Criterio de valoración probatoria de la sospecha grave...




