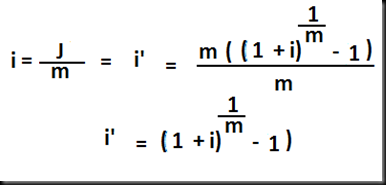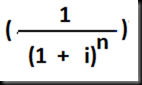Simbología
J= tasa anual dada convertible más de un año (tasa nominal)da clic para seguir el vinculo:
i= tasa de interés efectivamente ganada
n= número de periodos de interés
m= número de capitalizaciones en el año
i’= J/m = tasa de interés por periodo de interés o tasa proporcional
Ver más...
relación entre la tasa nominal y la tasa efectiva
tasa nominal
conversión de la tasa efectiva en tasa nominal
conversión de una tasa nominal en una tasa efectiva
tasa periódica o proporcional
tasa equivalente partiendo de una tasa efectiva
tasa de interés real